0. 텐서 연산
- 파이썬: 너무 느림
- NumPy
- Tensorflow: 딥러닝에 특화
- Keras: 텐서플로 기반으로 딥러닝 알고리즘도 구현함
1. 퍼셉트론
- Perceptron은 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 규칙에 따른 값을 출력한다.
- Perceptron에서는 '가중치'와 '편향'을 매개변수로 설정한다.
- Perceptron으로는 AND, OR gate 등의 논리 회로를 표현할 수 있다.
- XOR gate는 single-layer perceptron으로는 표현할 수 없다.
- 2층 perceptron을 이용하면 XOR gate를 표현할 수 있다.
- Single-perceptron은 직선형 영역만 표현할 수 있고, multi-layer perceptron은 비선형 영역도 표현할 수 있다.
2. 텐서
스칼라
차원이 없는 값
벡터
1차원
매트릭스(행렬)
2차원. (세로, 가로)로 나타냄
- 세로: batch size(행의 크기)
- 가로: dimension(열의 크기)
텐서
3차원 (또는 그 이상). (세로, 가로, 깊이)로 나타냄
- 세로: batch size
- 가로: width
- 깊이/높이: dimension
3. 넘파이(Numpy)
벡터, 매트릭스, 텐서 등 대규모 다차원 배열을 쉽게 다룰 수 있도록 많은 함수와 자료구조를 지원하는 파이썬 라이브러리
import numpy as np # 텐서 만들기: np.array() ## 리스트를 생성하여 np.array로 1차원 배열로 변환한다고 생각하면 쉬움 t = np.array([0., 1., 2., 3., 4., 5.]) print(t) # [0. 1. 2. 3. 4. 5.] # 차원 추출 t.ndim # 1 # 크기/모양 추출 t.shape # (7,) == (1, 7)인 벡터
넘파이 인덱스는 0 부터 시작한다. 인덱싱과 슬라이싱 가능.
4. 파이토치(PyTorch)
파이썬을 위한 오픈소스 머신러닝 라이브러리
import torch # 1차원(벡터) # 텐서 만들기: torch.Tensor() t = torch.FloatTensor([0., 1., 2., 3., 4., 5.]) # 차원 t.dim() # 1 # 크기 t.shape # torch.Size([7]) t.size() # torch.Size([7])
# 2차원(행렬) t = torch.FloatTensor([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.], [10., 11., 12.] ]) t.dim() # 2 t.size() # torch.Size([4, 3])
인덱스와 슬라이싱 모두 가능하다.
행렬의 곱
- 행렬 곱 (내적; matrix multiplication)
X.matmul(Y)# 예시 X = torch.rand(3, 2, 5) Y = torch.rand(3, 5, 3) D = X.matmul(Y) D.shape # torch.Size([3, 2, 3])
↳ (2, 5) 3개, (5, 3) 3개를 병렬로 곱해주는 연산을 한 것.
dim 0의 3은 batch size.
- 원소별로 곱하기
행렬의 크기가 같아야 한다.
X.mul(Y) X * Y
차원(dim)을 인자로 주는 경우
⇒ 해당 차원을 제거한다는 의미가 된다.
dim = 0: 행렬의 행
dim = 1: 행렬의 열
t = torch.FloatTensor([[1, 2], [3, 4]]) # tensor([[1., 2.], # [3., 4.]]) # 1) 원소 전체의 평균을 계산 t.mean() # tensor(2.5000) # 2) 첫번째 차원을 제거하며 평균을 계산 → 열의 평균 t.mean(dim=0) # tensor([2., 3.]) # 3) 두 번째 차원을 제거하며 평균을 계산 → 행의 평균 t.mean(dim=1) # tensor([1.5000, 3.5000]) ## 실제 연산 결과는 (2, 1)이지만, [x, x]로 차원이 축소되어 출력된다.
- 평균: mean()
- 덧셈: sum()
- 최대값: max()
- 최대값을 가진 인덱스: argmax()
max()에 dim 인자를 주면 argmax도 함께 반환한다:
t = torch.FloatTensor([[1, 2], [3, 4]]) t.max(dim=0) # (tensor([3., 4.]), tensor([1, 1])) ## dim=0: 첫 번째 차원을 제거 ## tensor([3., 4.]): 첫 번째 열에서 최대값 3., 두 번째 열에서 최대값 4. ## tensor([1, 1]): 첫 번째 열에서 3의 인덱스는 1, 두 번째 열에서 4의 인덱스는 1
view()
넘파이: reshape()
원소의 수를 유지하면서 텐서의 shape을 바꿔야 할 경우 사용한다.
- 원소의 개수는 변하지 않는다.
- 확실히 변경할 차원을 설정하고 다른 차원을 -1로 두면, -1로 둔 차원은 자동으로 조절된다. 즉, 사용자가 잘 모르겠으니 파이토치에 맡기겠다는 의미.
X = torch.rand(3, 2, 5) X.shape # torch.Size([3, 2, 5]) X.view(3, 10).shape # torch.Size([3, 10]) X.view(3, -1) # 3 * 2 * 5 = 3 * x, x = 10
브로드캐스팅 (Broadcasting)
크기가 다른 행렬의 크기를 자동으로 맞춰서 연산을 수행해주는 기능
각 dim에 대해 크기가 큰 쪽에 맞춰 반복 복제하여 크기를 맞춘다.
자동으로 실행되는 기능이므로, 편리한만큼 주의해서 사용해야 한다.
axis
다차원 텐서에서 함수 연산을 어떤 축으로 적용할지를 결정하기 위해 사용됨
참고자료는 여기
- axis=0 : row을 사라지는 기준으로. 가장 바깥쪽 bracket을 제거하여 계산.
- axis=1 : col을 사라지는 기준으로. 바깥에서 2번째 bracket을 제거하여 계산.
- axis=2 : depth을 사라지는 기준으로. 바깥에서 3번째 bracket을 제거하여 계산.
나머지 요소는 유지된다!
squeeze & unsqueeze
특정 차원이 1인 경우 축소시키거나(squeeze), 특정 차원을 1로 확장시킬 때(unsqueeze) 사용한다.
# squeeze X = torch.rand([100, 1, 20]) torch.squeeze(X) # X: [100, 1, 20] → [100, 20]
# unsqueeze X = torch.Tensor([0, 1, 2]) X.shape # torch.Size([3]) X.unsqueeze(0) # 첫 번째 차원(0)에 차원을 추가한다. # tensor([[0., 1., 2.]]) X.unsqueeze(0).shape # torch.Size([1, 3]) ## (3,)의 1차원 벡터가 (1, 3)의 2차원 텐서로 변경됨
type casting
텐서의 자료형을 변환하는 것
- .float() : 텐서에 붙여 float 형으로 변경
- .long() : long 형으로 변경
concatenate
두 텐서를 연결
torch.cat([])
- 인자로 dim을 전달하여 어느 차원을 늘릴 것인지 정할 수 있다.
x = torch.FloatTensor([[1, 2], [3, 4]]) y = torch.FloatTensor([[5, 6], [7, 8]]) torch.cat([x, y], dim=0) ## (2, 2) 2개 → (4, 2) # tensor([[1., 2.], # [3., 4.], # [5., 6.], # [7., 8.]]) torch.cat([x, y], dim=1) ## (2, 2) 2개 → (2, 4) # tensor([[1., 2., 5., 6.], # [3., 4., 7., 8.]])
stacking
연결하는 또 다른 방법. 쌓기.
a = torch.FloatTensor([0, 3]) b = torch.FloatTensor([1, 4]) c = torch.FloatTensor([2, 5]) torch.stack([x, y, z]) # tensor([[0., 3.], # [1., 4.], # [2., 5.]]) ## 앞에 있는 것이 위로 가도록 순차적으로 쌓인다.
ones_like, zeros_like
- ones_like : 동일한 크기의 1로만 채워진 텐서를 생성
- zeros_like : 동일한 크기의 0으로만 채워진 텐서를 생성
t = torch.FloatTensor([[0, 1, 2], [3, 4, 5]]) torch.ones_like(x) # tensor([[1., 1., 1.], # [1., 1., 1.]]) torch.zeros_like(x) # tensor([[0., 0., 0.], # [0., 0., 0.]])
덮어쓰기 연산
연산을 하더라도 기존의 값은 변경되지 않는다. 연산의 결과를 기존값에 저장하기 위해서는 연산 뒤에 _를 붙인다.
x = torch.FloatTensor([[1, 2], [3, 4]]) # 일반 x.mul(2.) # tensor([[2., 4.], [6., 8.]]) x # tensor([[1., 2.], [3., 4.]]) # 덮어쓰기 x.mul_(2.) # tensor([[2., 4.], [6., 8.]]) x # tensor([[2., 4.], [6., 8.]])
4. 선형 모델
선형 모델 에 대해, 주어진 데이터를 가장 잘 표현하는 parameter인 Weight 와 Bias 를 찾기!
산포도 그리기
import matplotlib.pyplot as plt # 데이터 x_train = torch.FloatTensor([[10], [11], [14], [18], [19], [22], [24]]) y_train = torch.FloatTensor([[45], [50], [55], [70], [58], [80], [85]]) X, Y = x_train, y_train #plot 입력 scatter = plt.scatter(X, Y) #X 및 Y 범위 설정 plt.xlim(X[0]-1, X[-1]+1) plt.ylim(Y.min()-1, Y.max()+1) #그래프의 타이틀과 x,y축 라벨링 plt.title('scatter', pad=10) plt.xlabel('X axis', labelpad=10) plt.ylabel('Y axis', labelpad=10) #틱설정 plt.xticks(np.linspace(X[0], X[-1], 11)) plt.yticks(np.linspace(np.min(np.append(Y,Y)), np.max(np.append(Y,Y)), 11)) plt.minorticks_on() plt.tick_params(axis='both', which='both', direction='in', pad=8, top=True, right=True) #플롯 출력 plt.show()
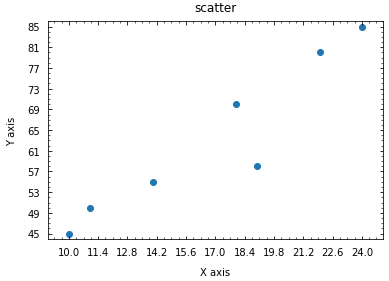
데이터 정제
- 데이터셋에 NaN 또는 null 이 있는지 체크: pandas 의 isnull()
import pandas as pd data_file.isnull()
- 미완성의 행을 제거: pandas 의 dropna()
data_file = data_file.dropna(axis=0).reset_index(drop=True) # axis=0: 행을 드롭하라 # reset_index: 인덱스 리셋
선형 그래프 그리기
iter = 50000 #loss값을 구하는 횟수로 총 50000번 weight_max = 100 #'[입력범위]'로 random값의 weight 범위 제한 목적 ( -50 < weight < 50 ) bias_max = 150 #오프셋으로 random값의 bias 범위 제한 목적 (-150 < bias < 0) min_loss = 1000000 #업데이트 된 가장 작은 값의 loss 저장 min_W = 0 min_b = 0 # iteration = 0 #dataset x = x_train y = y_train # 거짓 데이터에 강인하다고 알려진, L1 loss |hypothesis−y| 를 사용 def loss_fn(hypo, GT): return sum(abs(hypo - GT)) for i in range(iter): W = (torch.rand(1)-0.5) * weight_max b = (-torch.rand(1)) * bias_max hypothesis = W * x + b cur_loss = loss_fn(hypothesis,y) if cur_loss < min_loss: min_loss = cur_loss min_W = W min_b = b # iteration += 1 # print("iteration: ", iteration) # print("min_loss: ", min_loss) # print("min_W: ", min_W, " min_b: ", min_b)
# 직선 시각화 %matplotlib inline import matplotlib.pyplot as plt import numpy as np x = x_train y = y_train plt.scatter(x, y) t = np.arange(140.,190.,0.001) plt.plot(t, min_W*t+min_b) plt.xlabel('height (cm)') plt.ylabel('weight (kg)') plt.show()
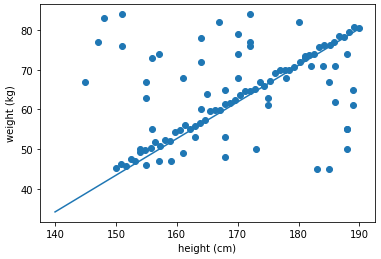
참조
'인공지능' 카테고리의 다른 글
| Linear Regression & Logistic Regression (0) | 2022.03.08 |
|---|---|
| [수학없는 인공지능] 인공지능의 역사와 기초 (0) | 2022.03.08 |
| [수학없는 인공지능] 퍼셉트론 (Perceptron)이란? (0) | 2022.03.08 |
| [수학없는 인공지능] 다층신경망 (Multi-layer Perceptron) (0) | 2022.03.08 |
| [수학없는 인공지능] 딥러닝 알고리즘 소개 (0) | 2022.03.08 |
