1. 기계학습에 대하여
🌱 Machine Learning — Fundamentals
1) 최적화와 일반화
최적화 (optimization)
input과 output이 주어지고, 그 관계를 가장 잘 설명하는 함수를 찾는 것.
- train data 에만 잘 fitting 되면 된다.
- Gradient Descent algorithm
: cost function을 에 대해 미분하여 cost가 낮아지는 방향으로 W를 조정하는 것.
일반화 (generalization)
train data와 다른, 새로운 input 에 대해서도 적절한 출력을 내보낸다면 일반화가 잘 이루어진 것이다.
- 최적화와는 달리, train data와는 별개로 test data를 가지고 함수가 새로운 데이터에도 잘 적용될 수 있도록 하는 것이다.
- 기계학습은 일반화까지를 포함한다.
2) 가장 좋은 모델 찾기
→ annotation을 통해 가능하다.
즉, 입력 데이터를 주고, 예측한 답을 정답과 비교하여, 오차를 측정하고 오차를 최소화하는 방향으로 최적화하는 것.
→ test를 통해 가장 좋은 결과를 내도록 하는 것.
(→ 기존 연구들에 대한 case study를 바탕으로 가장 적합할 것 같은 모델을 예상할 수도 있다.)
3) 용어
epoch
전체 train dataset을 한 번 도는 것
underfitting & overfitting
- underfitting: 너무 단순한 모델로 학습데이터도 잘 맞추지 못하는 경우
- overfitting: 너무 복잡한 모델로 학습데이터를 잘 맞추지만 새로운 데이터에서는 잘 기능하지 못하는 경우
- 방안:
- 충분히 많은 양의 데이터
- 모델의 복잡도 올리기 / 줄이기: feature의 수 줄이기 (overfitting의 경우)
- 가중치의 정규화(regularization) 적용하기
: 모델의 파라미터 값이 적절히 작은 값을 갖도록 억제하는 것 - 드롭아웃(drop out)
: 인공지능 신경망에서 중간중간 값들을 0으로 바꿔가면서 random effect 를 주는 것. 랜덤한 새로운 데이터가 들어오더라도 잘 처리할 수 있게끔 모델을 robust 하게 만들어주는 방법. - Early stopping

정규화 (normalization)
상관계수나 가중치가 너무 큰 값을 가지지 않도록 비용함수에 penalty 항을 더하는 것.
모델의 복잡도를 낮추기 위한 방법 (overfitting 문제 해소).
입력 feature의 차수가 높아질수록 모델의 복잡도가 증가하고 모든 데이터에 맞추려고 하는데, 고차항의 계수를 아주 작게 만들어 모델의 복잡도를 감소시킬 수 있다.
(가정) 가중치가 낮으면 모델의 복잡도가 단순해져 오버피팅을 피할 수 있다.
2. 지도학습
1) Linear Regression
독립변수에 대한 종속변수(주로 값)를 예측하기 위함!
데이터를 잘 설명하는 모델 파라미터를 찾기!
- 가설
(가정) 독립변수 x에 따른 종속변수 y의 상관관계가 선형적일 것이다.
$$ H(x)=Wx+b $$ - cost function: MSE(mean square error loss)
$$ cost(W, b) = \frac{1}{m} \sum^m_{i=1} \left( H(x^{(i)}) - y^{(i)}\right)^2 $$ - Gradient descent
가설의 결과와 정답의 차이를 미분하여(*back propagation), cost를 줄이는 방향으로 를 갱신하게 된다. 는 learning rate로, 한번에 얼마나 업데이트할지를 결정하는 하이퍼파라미터이다.
$$ W := W - \alpha \frac{\partial}{\partial W} cost(W) $$
- back propagation
"내가 뽑고자 하는 target값과 실제 모델이 계산한 output이 얼마나 차이가 나는지 구한 후 그 오차값을 다시 뒤로 전파해가면서 각 노드가 가지고 있는 변수들을 갱신하는 알고리즘인 것이다." 출처
- 코드
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# Weight와 bias
W = torch.zeros(1, requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# Data normalization: 0~1사이의 값들로 변경 (정규분포 생각하면 됨)
x_min, x_max = x_train.min(), x_train.max() # x의 최대, 최솟값
y_min, y_max = y_train.min(), y_train.max() # y의 최대, 최솟값
x = (x_train-x_min)/(x_max-x_min)
y = (y_train-y_min)/(y_max-y_min)
# optimizer 설정
## parameter는 리스트 형태로 넣었다.
optimizer = optim.SGD([W, b], lr=0.1)
# optimizer = optim.Adam([W, b], lr=0.1)
# 경사 하강법을 반복할 횟수 설정
epochs = 1000
for epoch in range(epochs + 1):
# H(x) 계산
hypothesis = W * x + b
# cost 계산: forward pass
cost = torch.mean((hypothesis - y) ** 2)
# cost로 H(x) 개선을 위한 update
## 기존 저장 gradient 리셋
# Zero gradients, perform a backward pass, and update the weights.
# 역전파 단계 전에, optimizer 객체를 사용하여 (모델의 학습 가능한 가중치인) 갱신할
# 변수들에 대한 모든 변화도(gradient)를 0으로 만듭니다. 이렇게 하는 이유는 기본적으로
# .backward()를 호출할 때마다 변화도가 버퍼(buffer)에 (덮어쓰지 않고) 누적되기
# 때문입니다. 더 자세한 내용은 torch.autograd.backward에 대한 문서를 참조하세요.
optimizer.zero_grad()
## cost에서 back propagation algorithm 으로 W, b에 대해 미분값 계산
# 역전파 단계: 모델의 매개변수들에 대한 손실의 변화도를 계산합니다.
# autograd 를 사용하여 역전파 단계를 계산합니다. 이는 requires_grad=True를 갖는
# 모든 텐서들에 대한 손실의 변화도를 계산합니다.
# 이후 a.grad와 b.grad, c.grad, d.grad는 각각 a, b, c, d에 대한 손실의 변화도를
# 갖는 텐서가 됩니다.
cost.backward()
## lr 만큼 W와 b를 한 스텝 갱신
# optimizer의 step 함수를 호출하면 매개변수가 갱신됩니다.
optimizer.step()
# (선택) 1000번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} W: {:.3f}, b: {:.3f} Cost: {:.6f}'.format(
epoch, epochs, W.item(), b.item(), cost.item()
))- 참고: Optimizer의 종류

[출처] 하용호, 자습해도 모르겠던 딥러닝, 머리속에 인스톨 시켜드립니다
2) Logistic Regression
데이터를 두 개의 그룹으로 분류하기 위함!
연속적인 값이 아니라 0 또는 1에 가까운 값으로 출력되는 분류 모델로, 데이터를 잘 구분하는 경계를 찾기!
Sigmoid function
종속변수(y)의 범위가 0과 1 사이이므로 경계를 급격하게 구분짓는 함수가 필요하게 되고, 여기에서 sigmoid 함수를 활용한다.
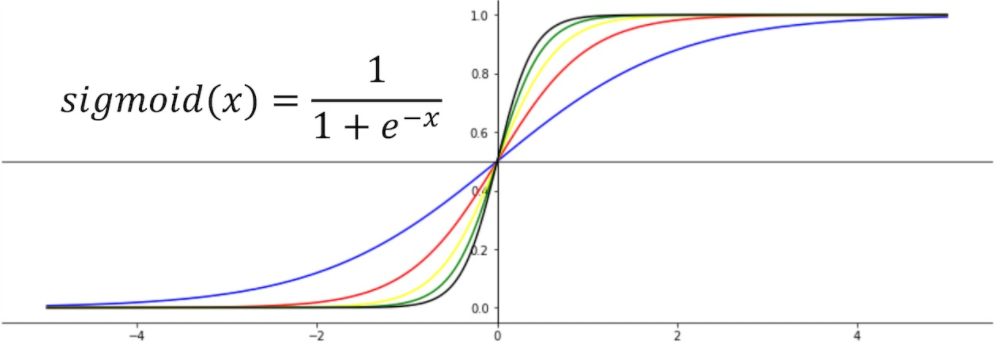
sigmoid 함수에 들어가는 의 값이 $$ z=ax $$
라고 할 때, 의 값이 커질수록 기울기가 가팔라져 step function(계단형 함수)에 가까워진다.
- 가설
$$ H(X) = \frac{1}{1+e^{-z}}$$, where $$z = W^T X + b $$
- cost function: binary cross-entropy
$$cost(W, b) = -\frac{1}{m} \sum y \log\left(H(x)\right) + (1-y) \left( \log(1-H(x) \right)$$
❓ binary cross-entropy를 사용하는 이유?
y가 1일때(두번째 항=0) H(x)가 0에 가까운 값이 나온다면, log(H(x))가 굉장히 큰 음수 값이 나온다.
y가 0일때(첫번째 항=0) H(x)가 1에 가까운 값이 나오면, log(1-H(x))가 큰 음수 값이 나온다.
즉, 예측값과 정답이 일치하지 않는 경우 전체 cost가 커지게 된다.
👻 음수값이 나오므로 (-) 부호를 붙여준다.
- Gradient descent
$$ W := W - \alpha \frac{\partial}{\partial W} cost(W) $$
- 코드
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
x_data = [[1, -4], [1, 2], [2, 3], [3, 1],[4, -2], [4, 3], [5, 3], [6, 2], [3, 8], [6, -2]]
y_data = [[0], [0], [0], [0], [0], [1], [1], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
# 모델 초기화
W = torch.zeros((2, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.Adam([W, b], lr=0.01)
nb_epochs = 5000
for epoch in range(nb_epochs + 1):
# hypothesis 계산
hypothesis = 1 / (1 + torch.exp(-(x_train.matmul(W) + b)))
# cost 계산
losses = -(y_train * torch.log(hypothesis) + (1 - y_train) * torch.log(1 - hypothesis))
cost = losses.mean()
# optimizer와 cost를 이용해 모델 파라메터 W,b를 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(epoch, nb_epochs, cost.item()))참조
'인공지능' 카테고리의 다른 글
| 텐서(tensor), 그리고 선형 모델 (0) | 2022.03.08 |
|---|---|
| [수학없는 인공지능] 인공지능의 역사와 기초 (0) | 2022.03.08 |
| [수학없는 인공지능] 퍼셉트론 (Perceptron)이란? (0) | 2022.03.08 |
| [수학없는 인공지능] 다층신경망 (Multi-layer Perceptron) (0) | 2022.03.08 |
| [수학없는 인공지능] 딥러닝 알고리즘 소개 (0) | 2022.03.08 |
