1. 최단 경로 알고리즘
세 가지 경우가 있다:
- (노드) 1 → 1
- 1 → all
- all → all
각각의 경우에 최적의 알고리즘을 찾을 수 있으며, 여기서는 하나의 노드에서 다른 모든 노드로 가는 경우를 보도록 한다.
Dijkstra 알고리즘
입력: 그래프 $G=$ {$V, E, W$}, $V=$ {$1, 2, 3, ..., n$}
출력: source 1에서 다른 정점으로의 최단 경로와 비용
$C[i, j]$: 연결선 $e=(i, j)$ 의 비용(가중치)
$D[i]$: source 1에서 정점 $i$ 까지 경로의 비용
$S=$ {$1$}
for $i=2$ to $n$
$D[i] = C[1, i]$ # 1에서 노드 $i$ 까지의 비용
while ($V≠S$)
$V-S$의 정점 중에서 $D[w]$가 최소값인 정점 $w$를 선택한다.
$w$를 $S$에 합한다. ($S=S+${$w$})
for $v∈V-S$ # $S$를 제외한 모든 정점들에 대해서
$D[v] = min(D[v]$, $D[w] + C[w, v])$
(즉, 각 단계에서 cost가 최소가 되는 정점을 택해서 그 정점을 이용해 더 최단 경로를 계속해서 갱신해나감. 직전의 노드를 기억함으로써 경로 구할 수 있다.)

- single-source 최단경로 알고리즘에 속한다: 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 찾음
- 방향/비방향 그래프에 모두 적용된다.
- 가중치 값이 음수가 아니어야 한다.
- 복잡도: $O(V^2)$ (구현에 따라 달라짐: $E*logV$)
- 용례: OSPF 라우팅 알고리즘
예시 코드
'''
5 11
0 1 3
0 2 5
1 2 2
1 3 6
2 1 1
2 3 4
2 4 6
3 4 2
3 5 3
4 0 3
4 5 6
'''
def dijkstra(s, V):
U = [0]*(V+1) # 비용이 결정된 정점을 표시
U[s] = 1 # 출발점 비용 결정
for i in range(V+1):
D[i] = adjM[s][i]
# 남은 정점의 비용 결정
for _ in range(V): # 남은 정점 개수만큼 반복
# D[w]가 최소인 w 결정, 비용이 결정되지 않은 정점w 중에서
minV = INF
w = 0
for i in range(V+1):
if U[i] == 0 and minV > D[i]:
minV = D[i]
w = i
U[w] = 1 # 비용 결정
for v in range(V+1):
if 0< adjM[w][v]< INF:
D[v] = min(D[v], D[w]+adjM[w][v])
INF = 10000
V, E = map(int, input().split())
adjM = [[INF]*(V+1) for _ in range(V+1)]
for i in range(V+1):
adjM[i][i] = 0
for _ in range(E):
u, v, w = map(int, input().split())
adjM[u][v] = w
D = [0]*(V+1)
dijkstra(0, V)
print(D)
인접리스트로 구현
'''
5 11
0 1 3
0 2 5
1 2 2
1 3 6
2 1 1
2 3 4
2 4 6
3 4 2
3 5 3
4 0 3
4 5 6
'''
def dijkstra(s, V):
U = [0]*(V+1) # 비용이 결정된 정점을 표시
U[s] = 1 # 출발점 비용 결정
D[s] = 0
for v, w in adjL[s]:
D[v] = w
# 남은 정점의 비용 결정
for _ in range(V): # 남은 정점 개수만큼 반복
# D[t]가 최소인 t 결정, 비용이 결정되지 않은 정점t 중에서
minV = INF
t = 0
for i in range(V+1):
if U[i] == 0 and minV > D[i]:
minV = D[i]
t = i
U[t] = 1 # 비용 결정
for v, w in adjL[t]:
D[v] = min(D[v], D[t]+w)
INF = 10000
V, E = map(int, input().split())
adjL = [[] for _ in range(V+1)]
for _ in range(E):
u, v, w = map(int, input().split())
adjL[u].append([v, w])
D = [INF]*(V+1)
dijkstra(0, V)
print(D)Bellman-Ford 알고리즘
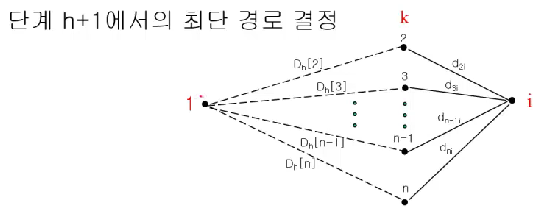
source로부터 특정 정점에 이르는 경로를 선택할 때,
각 단계 $h$마다 최대 $h$ 개의 연결선으로 연결된 경로 중에서 최소값을 갖는 경로를 선택
$D_h[k]$: $h$ 단계까지 계산 결과 source 1에서 각 정점에 이르는 경로의 최소값
$d_{ki}$: 연결선 ($k, i$)의 비용
→ $D_h[k] + d_{ki}$ 를 계산하여 최소값 선택 (직접 연결된 경로에 대해, 그 경로의 비용 + 직전 단계까지의 비용)
입력: 그래프 $G=$ {$V, E, W$}, $V=$ {$1, 2, 3, ..., n$}
출력: source 1에서 다른 정점으로의 최단 경로와 비용
[단계 1] 초기화
$D[1] = 0, D[i] = ∞$ for all $i∈${$2, 3, ..., n$}
[단계 2]
for all $i∈${$2, 3, ..., n$}
$D[i] = min(D[k] + d_{ki})$ for $i$ 와 직접 연결선이 있는 $k$
단계 2'의 절차를 $D[i]$ 의 변화가 더 이상 발생하지 않을 때까지 반복한다.
($i$ 노드와 연결되어 있는 노드 $k$ 각각에 대해, 노드 $i$에서 $k$까지 이르는 거리에 노드 1에서 노드 $k$ 까지 이르는 거리를 합하여, 그 중 최소값으로 갱신한다. 한 회차 당 모든 노드에 대해 이를 수행한다.)

- single source에서 모든 정점까지의 최단 거리 결정
- 방향/비방향 그래프에 모두 적용
- 가중치가 음수일 때도 적용 가능
- 하지만, (같은) 순환을 구성하는 연결선의 가중치의 합은 양수여야 한다.
- 용례: 인터넷의 라우팅 프로토콜에서 사용: RIP, BGP
- 복잡도
- 실제 계산은 매 단계에서 앞 예제의 테이블에 있는 각 정점에 대하여 모든 연결선의 비용을 다시 계산하고 업데이트한다.
- 따라서, $O(V*E)$
참조
'알고리즘' 카테고리의 다른 글
| 문자열(string): 브루트 포스, KMP, 보이어-무어 (0) | 2022.03.11 |
|---|---|
| 스택(Stack) (0) | 2022.03.11 |
| 재귀(recursion): 부분집합의 합, 순열 (0) | 2022.03.10 |
| 최소 신장 트리(MST): Prim, Kruskal (0) | 2022.03.10 |
| DFS 살펴보기 🚲 (0) | 2022.03.10 |
